library(cmdstanr) # for fitting Bayesian models
library(fixest) # Fitting fixed effects modelsFixed effects and Bayesian Multi-level models
This is one of those posts I made mainly so that I have something to link to whenever I get this particular question.
The punchline
Consider a model with unobserved heterogeneity \(a_i\):
\[y_{i,t} = a_i + a_1 * x_{i,t} + u_{i,t}, \,\, \, \, \, cov(a_i, x_{i,t}) \ne 0\]
\(a_i\) is meant to denote unobservable subject-specific heterogeneity that is confounding the relation of interest between \(y\) and \(x\) (because \(cov(a_i, x_{i,t}) \ne 0\)). Fixed effects models, as commonly used in econometrics, remove between-subject variation to estimate the coefficient of interest (\(a_1\)) using only within-variation. In the remainder of this short note, I assume that readers are similar with these type of fixed effects models.
Bayesian multi-level models can also account for \(a_i\), but one needs to consider that Bayesian multi-level models partially pool. Meaning, if one does not explicitly tell the model that there is a correlation between \(a_i\) and \(x_{i,t}\), then it will partially pool the confounded between-variation and the within-variation. Incorporating this correlation is easy to do however. This note shows how.
Setup
Simulated data
For illustration purposes I simulate data from the following data generating process:
\[a_i \sim N(2, 4)\]
\[x_{i,t} \sim 1.4 * a_i + N(0, 4)\]
\[y_{i,t} \sim a_i + 1 * x_{i,t} + N(0, 4)\]
So, the true value of \(a_1\) will be one in this simulation.
set.seed(753)
n_firms <- 100
periods <- 7
firm_id <- rep(1:n_firms, each = periods)
firm_mean <- rnorm(n_firms, 2, 4)
d <- data.frame(
firm_id = firm_id,
period = rep(1:periods, times = n_firms),
firm_mean = rep(firm_mean, each = periods)
)
# x is a function of the firm mean unobserved firm means
d$x <- rnorm(n_firms * periods, 0, 4) + 1.4 * d$firm_mean
# true coefficient of interest on x is 1
d$y <- d$firm_mean + 1 * d$x + rnorm(n_firms * periods, 0, 4)
# data container for bayesmodel
input_data <- list(
N = nrow(d),
J = max(d$firm_id),
GroupID = d$firm_id,
y = d$y,
x = d$x,
xm =
aggregate(
cbind(x) ~ firm_id,
data = d,
FUN = \(h) c(mean = mean(h))
)$x
)Confounded pooled OLS estimate
Unsurprising, normal OLS will yield biased estimates because \(cov(a_i, x_{i,t}) \ne 0\):
summary(lm(y ~ x, data = d))$coefficients Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6940142 0.19296977 3.596492 3.452875e-04
x 1.4855348 0.02437638 60.941562 1.120002e-281Fixed effect estimate
For comparison purposes with the Bayesian models, here are the estimates of standard fixed effects models:
Using the fixestpackage:
olsfe <- feols(y ~ x | firm_id, data = d)
summary(olsfe)OLS estimation, Dep. Var.: y
Observations: 700
Fixed-effects: firm_id: 100
Standard-errors: Clustered (firm_id)
Estimate Std. Error t value Pr(>|t|)
x 1.02745 0.044027 23.3367 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 3.75528 Adj. R2: 0.878907
Within R2: 0.534057The above fixed effects models yield estimates of 1.027, close to the true value of \(a_1 = 1\). Just as expected.
Simple Bayesian multi-level model
In contrast to fixed effects models, which throw away between-subject-variation, Bayesian multi-level models model \(a_i\) directly. In addition, these models have the advantage of applying adaptive shrinkage via partial pooling. This results in more stable and robust estimates of \(a_i\).
The model below does partial pooling by assuming that the \(a_i\) follow a common distribution.
\[ a_i = \mu_a + N(0, \sigma_a)\]
But it does not consider that \(a_i\) and \(x_{i,t}\) might be correlated. As a result the coefficient on x will be the partially pooled average of the between- and within-subject variation:
baymod_nocorr <- "
data{
int<lower=1> N; // num obs
int<lower=1> J; // num groups
int<lower=1, upper=J> GroupID[N]; // GroupID for obs, e.g. FirmID or Industry-YearID
vector[N] y; // Response
vector[N] x; // Predictor
}
parameters{
vector[J] z; // standard normal sampler
real mu_a; // hypprior mean coefficients
real<lower=0> sig_u; // error-term scale
real<lower=0> sig_a; // error-term scale
real a1;
}
transformed parameters{
vector[J] ai; // intercept vector
ai = mu_a + z * sig_a;
}
model{
z ~ normal(0, 1);
mu_a ~ normal(0, 10);
sig_u ~ exponential(1.0 / 8);
sig_a ~ exponential(1.0 / 4);
a1 ~ normal(0, 10);
y ~ normal(ai[GroupID] + a1 * x, sig_u);
}
"
stanmod_nocorr <- cmdstan_model(write_stan_file(baymod_nocorr))
bayfit_nocorr <- stanmod_nocorr$sample(
data = input_data,
iter_sampling = 1000,
iter_warmup = 1000,
chains = 4,
parallel_chains = 4,
seed = 1234,
refresh = 0
)Running MCMC with 4 parallel chains...
Chain 1 finished in 0.7 seconds.
Chain 2 finished in 0.7 seconds.
Chain 3 finished in 0.7 seconds.
Chain 4 finished in 0.8 seconds.
All 4 chains finished successfully.
Mean chain execution time: 0.7 seconds.
Total execution time: 0.9 seconds.bayfit_nocorr$summary(variables = c("a1", "mu_a", "sig_a", "sig_u"))# A tibble: 4 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <num> <num> <num> <num> <num> <num> <num> <num> <num>
1 a1 1.32 1.32 0.0499 0.0500 1.24 1.40 1.00 765. 1330.
2 mu_a 1.24 1.23 0.319 0.315 0.730 1.77 1.00 1243. 2228.
3 sig_a 2.25 2.26 0.399 0.403 1.60 2.90 1.00 658. 902.
4 sig_u 4.25 4.25 0.137 0.138 4.04 4.48 1.00 1528. 2219.Here is a visual presentation of the posterior of \(a_1\)
bayesplot::mcmc_areas(bayfit_nocorr$draws("a1")) + ggplot2::xlim(0, 2)
Bayesian multi-level model explicitely modelling correlation x and ai
This model gets rid of the problem, simply by explicitly modelling the correlation between \(a_i\) and between-firm variation in \(x_{i,t}\) as:
\[ a_i = \mu_a + b * \bar x_i + N(0, \sigma_a)\] \(b\) will be the estimate of the between association, while \(a1\) estimates the within-variation. We still get shrinkage of \(a_i\) around the between variation.
baymod_corr <- "
data{
int<lower=1> N; // num obs
int<lower=1> J; // num groups
int<lower=1, upper=J> GroupID[N]; // GroupID for obs, e.g. FirmID or Industry-YearID
vector[N] y; // Response
vector[N] x; // Predictor
vector[J] xm; // mean of x for groupID
}
parameters{
vector[J] z; // standard normal sampler
real mu_a; // hypprior mean coefficients
real<lower=0> sig_u; // error-term scale
real<lower=0> sig_a; // error-term scale
real a1;
real b;
}
transformed parameters{
vector[J] ai; // intercept vector
ai = mu_a + b * xm + z * sig_a;
}
model{
z ~ normal(0, 1);
mu_a ~ normal(0, 10);
sig_u ~ exponential(1.0 / 8);
sig_a ~ exponential(1.0 / 8);
a1 ~ normal(0, 10);
b ~ normal(0, 10);
y ~ normal(ai[GroupID] + a1 * x, sig_u);
}
"
stanmod_corr <- cmdstan_model(write_stan_file(baymod_corr))
bayfit_corr <- stanmod_corr$sample(
data = input_data,
iter_sampling = 1000,
iter_warmup = 1000,
chains = 4,
parallel_chains = 4,
seed = 123334,
refresh = 0
)Running MCMC with 4 parallel chains...
Chain 4 finished in 1.1 seconds.
Chain 2 finished in 1.1 seconds.
Chain 1 finished in 1.2 seconds.
Chain 3 finished in 1.2 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.1 seconds.
Total execution time: 1.3 seconds.bayfit_corr$summary(variables = c("a1", "b", "mu_a", "sig_a", "sig_u"))# A tibble: 5 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <num> <num> <num> <num> <num> <num> <num> <num> <num>
1 a1 1.03 1.03 0.0398 0.0392 0.961 1.09 1.00 3064. 2765.
2 b 0.652 0.652 0.0490 0.0490 0.572 0.732 1.00 3228. 2923.
3 mu_a 0.0616 0.0622 0.191 0.188 -0.251 0.375 1.00 3717. 2651.
4 sig_a 0.631 0.644 0.311 0.332 0.0939 1.13 1.00 749. 1487.
5 sig_u 4.08 4.07 0.119 0.118 3.88 4.27 1.00 3050. 2722.\(a1\) is now centered on the true value.
bayesplot::mcmc_areas(bayfit_corr$draws("a1")) + ggplot2::xlim(0, 2)
Another way of encoding the correlation between ai and x
The next piece of code more closely resembles the causal flow as I envision it. It encodes \(\bar x_i \sim b0 + b1 * a_i + e_{x,i}\). It fully recovers the simulation above (see the estimates of sig_a). The divergent transitions suggest that this model is harder to fit well. Not sure why that is. Something to figure out another day.
baymod_corr2 <- "
data{
int<lower=1> N; // num obs
int<lower=1> J; // num groups
int<lower=1, upper=J> GroupID[N]; // GroupID for obs, e.g. FirmID or Industry-YearID
vector[N] y; // Response
vector[N] x; // Predictor
vector[J] xm; // mean of x for groupID
}
parameters{
vector[J] z; // standard normal sampler
real mu_a; // hypprior mean coefficients
real<lower=0> sig_u; // error-term scale
real<lower=0> sig_a; // error-term scale
real<lower=0> sig_x; // error-term scale
real a1;
real b1;
real b0;
}
transformed parameters{
vector[J] ai; // intercept vector
ai = mu_a + z * sig_a;
}
model{
z ~ normal(0, 1);
mu_a ~ normal(0, 10);
sig_u ~ exponential(1.0 / 8);
sig_a ~ exponential(1.0 / 8);
a1 ~ normal(0, 10);
b1 ~ normal(0, 10);
b0 ~ normal(0, 10);
sig_x ~ exponential(1.0 / 7);
xm ~ normal(b0 + b1 * ai, sig_x);
y ~ normal(ai[GroupID] + a1 * x, sig_u);
}
"
stanmod_corr2 <- cmdstan_model(write_stan_file(baymod_corr2))
bayfit_corr2 <- stanmod_corr2$sample(
data = input_data,
iter_sampling = 1000,
iter_warmup = 1000,
adapt_delta = 0.9,
chains = 4,
parallel_chains = 4,
seed = 123244,
refresh = 0
)Running MCMC with 4 parallel chains...
Chain 2 finished in 1.3 seconds.
Chain 1 finished in 1.4 seconds.
Chain 4 finished in 1.8 seconds.
Chain 3 finished in 2.0 seconds.
All 4 chains finished successfully.
Mean chain execution time: 1.6 seconds.
Total execution time: 2.0 seconds.bayfit_corr2$summary(variables = c("a1", "b0", "b1", "mu_a", "sig_a", "sig_u", "sig_x"))# A tibble: 7 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <num> <num> <num> <num> <num> <num> <num> <num> <num>
1 a1 1.03 1.03 0.0395 0.0399 0.968 1.10 1.00 1068. 1501.
2 b0 0.00162 0.00387 0.296 0.286 -0.481 0.496 1.01 1381. 1993.
3 b1 1.52 1.51 0.119 0.120 1.34 1.72 1.00 682. 523.
4 mu_a 2.17 2.15 0.445 0.464 1.45 2.91 1.04 134. 444.
5 sig_a 3.97 3.96 0.399 0.398 3.36 4.66 1.01 333. 661.
6 sig_u 4.07 4.07 0.113 0.115 3.88 4.26 1.01 1188. 1738.
7 sig_x 1.08 1.08 0.368 0.398 0.507 1.70 1.06 119. 168.bayesplot::mcmc_areas(bayfit_corr2$draws("a1")) + ggplot2::xlim(0, 2)
Why bother with a Bayesian model if the OLS fixed effects ones work?
Two reasons:
- Precision and estimates of \(a_i\)
- Often multi-level models are used for more complicated situations than the one described here. Mostly for modelling heterogeneity in responses. In those situations it can still be important to acknowledge correlations with unobserved \(a_i\).
Comparing FE estimates
a_i_summary <- bayfit_corr$summary(variables = c("ai"))
a_i_summary2 <- bayfit_corr2$summary(variables = c("ai"))yrange <- range(c(fixef(olsfe)$firm_id, a_i_summary$mean, a_i_summary2$mean))
wblue <- rgb(85, 130, 169, alpha = 90, maxColorValue = 255)
par(mfrow = c(1, 3), pty="s", tck = -.02, oma = c(1, 1, 1, 1), mar = c(4, 3, 1, 1))
plot(firm_mean, fixef(olsfe)$firm_id, pch = 19, col = wblue, ylim = yrange,
ylab = "OLS FE estimate", xlab = expression("True "*a[i]))
abline(a = 0, b = 1, col = "grey")
plot(firm_mean, a_i_summary$mean, pch = 19, col = wblue, ylim = yrange,
ylab = "Bayes posterior mean 1", xlab = expression("True "*a[i]))
abline(a = 0, b = 1, col = "grey")
plot(firm_mean, a_i_summary2$mean, pch = 19, col = wblue, ylim = yrange,
ylab = "Bayes posterior mean 2", xlab = expression("True "*a[i]))
abline(a = 0, b = 1, col = "grey")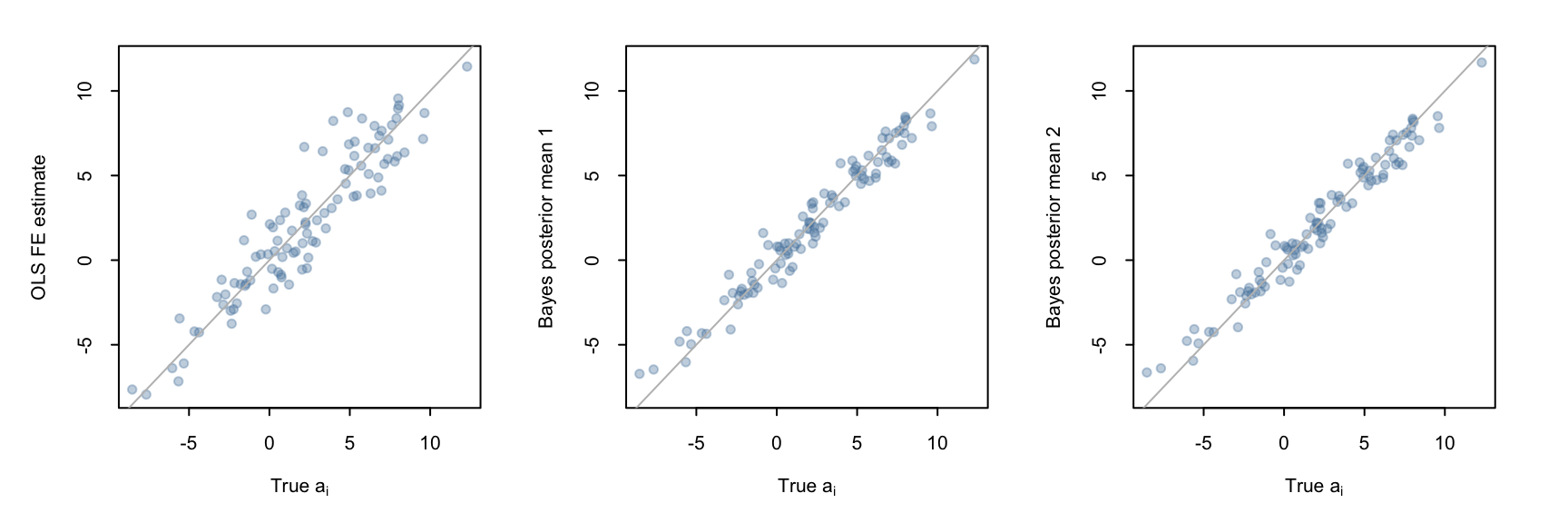
As we can see, the Bayesian estimates are less noisy than the OLS ones.
We can also see the same thing by comparing the differences between the \(a_i\) estimates and the true firm mean values:
data.frame(
bay1 = a_i_summary$mean - firm_mean,
bay2 = a_i_summary2$mean - firm_mean,
ols = fixef(olsfe)$firm_id - firm_mean
) |>
summary() bay1 bay2 ols
Min. :-1.732067 Min. :-1.830365 Min. :-2.858362
1st Qu.:-0.647746 1st Qu.:-0.728263 1st Qu.:-1.155375
Median : 0.022125 Median :-0.004072 Median :-0.008425
Mean :-0.003507 Mean :-0.028118 Mean :-0.005805
3rd Qu.: 0.480510 3rd Qu.: 0.487135 3rd Qu.: 0.903697
Max. : 2.447100 Max. : 2.382485 Max. : 4.523085